In this blog, we will discuss the surface area of a cylinder. Do you know what a cylinder is? Yes, of course, water bottles, pens, jars, bamboo, etc are examples of the cylinder.

 

 

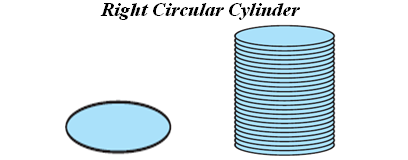
But I want to introduce the right circular cylinder. If we take a number of circular sheets of paper and stack them up what would we get? Here, if the stack is kept vertically up, we get what is called a right circular cylinder, since it has been kept at right angles to the base, and the base is circular.

Take a rectangular sheet. Let us roll it. It turns into a cylindrical shape. The line joining the center of the circle is called the axis of the cylinder. The area of the sheet gives us the curved surface area of the cylinder. Observe that the length of the sheet is equal to the circumference of the circular base which is equal to 2?r.

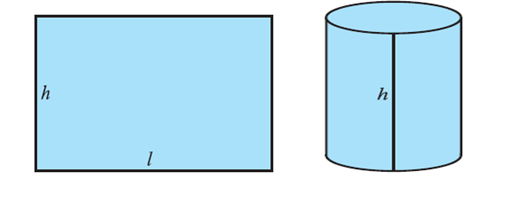
So, the curved surface area of the cylinder = area of the rectangular sheet = length � breadth
= perimeter of the base of the cylinder � h = 2?r � h = 2r?h, where r is the radius of the base of the cylinder and h is the height of the cylinder

Here we haven�t considered the top and the base of the cylinder. Look at this bottle a closed cylinder. Let us open it. On opening, we can observe that we have a rectangle and 2 circles. If the top and the bottom of the cylinder are also to be covered, then we need two circles (in fact, circular regions) to do that, each of radius r.

 

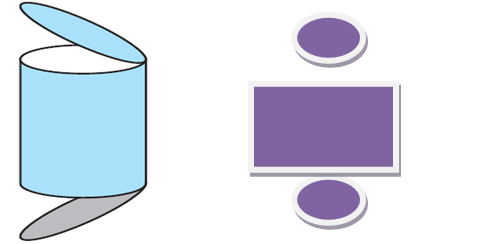
Thus having an area of ?r2 each giving us the total surface area as curved surface area + area of 2 circles = 2?rh + 2?r2 = 2?r(r + h). So, Total Surface Area of a Cylinder = 2?r(r + h) where h is the height of the cylinder and r its radius.

Examples of Surface Area Of A Cylinder

Savitri had to make a model of a cylindrical kaleidoscope for her science project. She wanted to use chart paper to make the curved surface of the kaleidoscope. What would be the area of chart paper required by her, if she wanted to make a kaleidoscope of length 25 cm with a 3.5 cm radius? You may take ?= 22/7

 

Solution: Radius of the base of the cylindrical kaleidoscope (r) = 3.5 cm.
Height (length) of kaleidoscope (h) = 25 cm.
Area of chart paper required = curved surface area of the kaleidoscope
= 2?rh
= 2x 22/7 x3.5x25 cm square
= 550 cm square

Let's understand the volume of cylinder. Just as a cuboid is built up with rectangles of the same size, a right circular cylinder can be built using circles of the same size. So, using the same argument as for a cuboid, we can see that the volume of a cylinder can be obtained as :

base area � height = area of circular base � height = ?r²h
The volume of a Cylinder = ?r²h, where r is the base radius and h is the height of the cylinder.

Volume of a Cylinder = ?r²h

1. Let us take an example The pillars of a temple are cylindrically shaped. If each pillar has a circular base of a radius of 20 cm and a height of 10 m, how much concrete mixture would be required to build 14 such pillars?

Solution: Since the concrete mixture that is to be used to build up the pillars is going to occupy the entire space of the pillar, what we need to find here is the volume of the cylinders.
The radius of the base of a cylinder = 20 cm.
Height of the cylindrical pillar = 10 m = 1000 cm
So, volume of each cylinder = ?r²h that is 22/7 into20 into 20 into 1000cm. On solving it gives 8800000cmcube or = 8.8/ 7m³

Therefore, the volume of 14 pillars = volume of each cylinder � 14
=8.8/7 into 14?m cube
= 17.6 m cube
So, 14 pillars would need a 17.6 m cube of a concrete mixture.

 

2. At a Ramzan Mela, a stall keeper in one of the food stalls has a large cylindrical vessel of base radius 15 cm filled up to a height of 32 cm with orange juice. The juice is filled in small cylindrical glasses of radius 3 cm up to a height of 8 cm and sold for Rs 3 each. How much money does the stall keeper receive by selling the juice completely?

Solution: The volume of juice in the vessel = volume of the cylindrical vessel = ?R²H (where R and H are taken as the radius and height respectively of the vessel). = ?� 15 � 15 � 32 cm³

 

 

Read More- Volume of a Cone: Definition, Formula, Derivation, and Solved Examples