While rationality meaning is �reason� in common usages, however, in mathematics the meaning of rational comes from the word �ratio� i.e. the rational number is a ratio between integers. Rational numbers are in the form p/q, where p and q are integers and q is not equal to zero. Because of the basic structure of numbers, p/q form, most people find it difficult to distinguish between fractions and rational numbers. Whole numbers make up fractions, whereas integers make up the numerator and denominator of rational numbers. 

 

If we attempt to define rational numbers further it will be:

 

Any number that can be written in the form fraction i.e. x/y where x and y must be integers but y?0

 

Rational Number Definition

 

A rational number has the form p/q, where p and q are both integers and q is not equal to 0. Q stands for the set of rational numbers. In other terms, a number is a rational number if it can be written as a fraction with both the numerator and denominator being integers.

 

Example of Rational Numbers

 

6/8 can be called a rational number because both 6 and 8 are integers -17/19 is also a rational number because both -17 and 19 are integers 4.5 can be written as 45/10=9/2 where both 9 and 2 are integers

 

Rational numbers also include all those decimal numbers that can be expressed in the form of fractions.

 

Example:

 

1. -17.65 can be written as -1765/100=-353/20 where both -353 and 20 are integers.

 

Rational Numbers Examples:

 

 

Rational Numbers as Part of Number System:

 

 

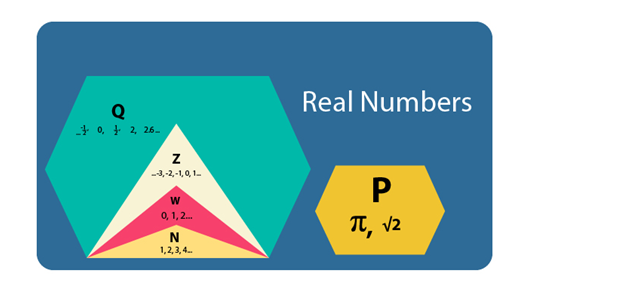
When we talk about the number system it can be thought of as a large set that has different kinds of numbers, as depicted in the diagram below:

 

1. Natural Numbers (N) � 1,2,3,��..are all those numbers that you use for counting objects around you, and i.e. why these are also known as counting numbers.

 

2. Whole Numbers (W) � 0,1,2,3,4��.i.e 0 added to the set of natural numbers gives you whole numbers

 

3. Integers (Z) - �..-5,-4,-3,-2,-1,0,1,2,3,4,5��..i.e negative values of all natural numbers together with whole numbers form integers.

 

4. Rational Numbers (Q): All those real numbers that include not just the natural numbers, whole numbers, integers but also all those numbers that can be written in the form of fraction eg. 9/8,-3/5 or in the form of decimal eg. 5.367666,-4.65, etc.

 

5. Irrational numbers (P): All those real numbers which cannot be expressed as a fraction eg. values of ?(pi), ?2 (square root of 2), etc

 

Properties of Rational Numbers:

 

1. Closure Properties:

 

(a.) Rational numbers are closed under addition i.e. for an equation p+q=r. If p and q are rational numbers then their sum i.e. r is also a rational number.

 

Example:

 

Since 3/2 and 2/9 are rational numbers, their sum i.e. 3/2 + 2/9 = 31/18 is also a rational number.

 

(b.) Rational numbers are closed under subtraction i.e. for an equation p-q=r. If p and q are rational numbers then their difference i.e. r is also a rational number.

 

Example:

 

Since 4/5 and 11/5 are rational numbers, their difference i.e. 4/5 � 11/5 = -7/5 is also a rational number.

 

(c.) Rational numbers are closed under multiplication i.e. for an equation p * q = r. If p and q are rational numbers then their product i.e. r is also a rational number.

 

Example:

 

Since 0/8 and -14/28 are rational numbers, their product i.e. 0/8 * -14/28 = 0 is also a rational number.

 

(d.) However, rational numbers are not closed under division i.e. division of 2 rational numbers may not always yield a rational number.

 

Example:

 

Both 5 and 0 are rational numbers, but their division i.e. 5/0 is not defined.

 

2. Commutativity Property:

 

(a.) Addition and multiplication are commutative for rational numbers i.e.

 

x + y = y + x and x * y = y * x

 

Examples:

 

If x = -2/5 and y = 11/5 then,

 

-2/5 + 11/5 = 9/5 = 11/5 + (� 2/5)

 

and -2/5 * 11/5 = -22/25 = 11/5 * -2/5

 

(b.) Subtraction and division are not commutative for rational numbers

 

i.e. a � b ? b � a and a � b ? b � a

 

Examples:

 

If a = 2/3 and b = 5/4 then, 2/3 - 5/4 = -7/12 but, 5/4 -2/3 = 7/12

 

2/3 � 5/4 = 8/15 but, 5/4 � 2/3 = 15/8

 

3. Associativity:

 

(a.) Addition and multiplication are associative for rational numbers i.e.

 

(x + y) + z = x + (y + z) and (x * y) * z = x * (y * z)

 

Examples:

 

If x = -2/3, y = 3/5 and z = -5/6 then,

 

(-2/3 + 3/5) + (-5/6) = -9/10 = -2/3 + [3/5 + (-5/6)]

 

(-2/3 * 3/5) * (-5/6) = 1/3 = -2/3 * [3/5 * (-5/6)]

 

(b.) Subtraction and division are not associative for rational numbers i.e.

 

(a � b) - c ? a � (b � c) and (a � b) � c ? a � (b � c)

 

Examples:

 

If a = 3/5, b = -17/5, c = 20/5 then,

 

[3/5 � (-17/5)] � 20/5 = 0 but, 3/5 � [(-17/5) � 20/5] = 8

 

[3/5 � (-17/5)] � 20/5 = -3/68 but, 3/5 � [(-17/5) �20/5] = -12/17

 

What is Known as the Standard Form of Rational Number?

 

If p/q is a rational number such that: p is any integer and q is a positive integer and there is no common factor between them other than 1. Then this p/q is said to be a rational number in its standard form.

 

Examples:�-9/7, 7/2, 16/15, -10/7

 

Read More: What Is Circle

 

FAQs